Sampling is a very complex problem but the basics are not all that difficult to understand. We’re simply taking samples of things, audio signals in this case, at a particular rate and resolution (terms to be defined in context shortly). Let’s start with the Shannon Sampling Theory, the basis for digital audio:
“If a function of time f(t) contains no frequencies higher than W Hertz, it is completely determined by giving the value of the function at a series of points spaced 1/2W seconds apart.”
Claude Shannon was researching information theory and the most efficient ways to transmit and recover information. Harry Nyquist, a controls expert, refined the theorem and gave us the well-known Nyquist frequency limit: the maximum bandwidth that can be captured by sampling at frequency fs is fbw < fs/2.
A few comments on the sampling theorem:
Most ADCs first convert a signal into discrete (quantized) time values using a track-and-hold (T/H) circuit, then quantize the amplitude to produce a digital signal. Thus we go from signals continuous in time and amplitude, to discrete time and continuous amplitude, and finally to digital signals having discrete time and amplitude. An ADC typically includes the T/H so we don’t see that intermediate step. However, sampling errors in time and amplitude are important in achieving a high-quality digital result.
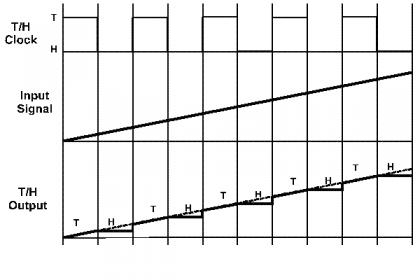
The figure below shows a ramp input signal before (middle) and after (bottom) sampling by a T/H. The clock is high to track the signal, and low to hold. A perfect T/H instantly follows the signal when in track mode, and perfectly maintains the signal value in hold mode. There are a myriad of non-ideal effects in real systems including noise, nonlinearity (distortion), clock and signal feed through, finite bandwidth and acquisition time, hold-mode droop, glitches when changing state, etc. For now, just knowing what happens in a T/H is enough. Not all ADCs include a T/H, combining time sampling with amplitude quantization in one step. (Click on the figure to see bigger -- I shrunk them down to upload.)
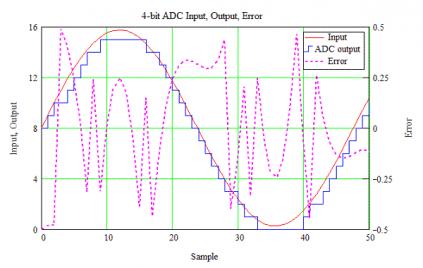
After the T/H a quantizer converts the held values to discrete amplitude values. The resolution of the quantizer, and thus the complete ADC, is expressed in bits – numbers to the base two. One bit has two levels (2^1 = 2); four bits, 16 levels (2^4), etc. A 16-bit ADC has 65,536 discrete amplitude steps – quite a few, but a long way from infinite. The figure below shows a 1 kHz signal sampled at 44.1 kS/s (44.1 kHz, CD rate) by a 4-bit ADC. Very low resolution, but makes it easy to see what happens. The input is in red and output in blue. The output has levels from 0 to 15 (16 different values, or least-significant bits, lsbs). The error signal (dashed line) ties to the right-hand Y axis and for this perfect ADC ranges from -0.5 to +0.5 lsbs. Note the random appearance of the error signal; for an ideal ADC this is very close to (and generally treated as) simple white noise. This error is the quantization noise.
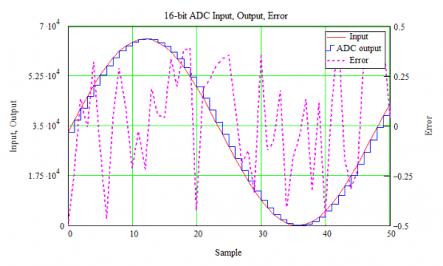
Stepping up to 16 bits give us the plot below. The number of steps is the same because the sampling time has not changed. However, the amplitude resolution is much finer (notice the output more closely follows the input). The error curve is a bit misleading since it is in lsbs; the error is actually only 1/4096 the size of the 4-bit ADC’s error! (The difference between 4 and 16 bits is 12 bits, and 2^12 = 4096.) I thought about plotting the two error curves together, but by eye the 16-bit error is essentially a flat line at the same scale as the 4-bit error signal.
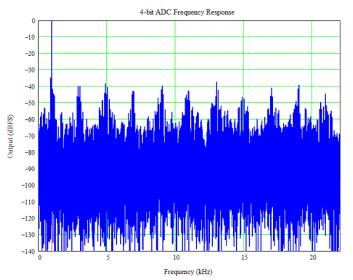
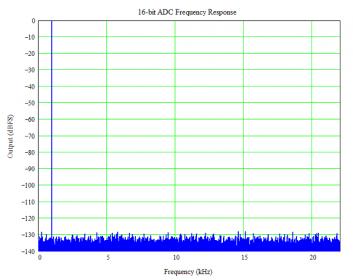
To really see the difference in resolution, let’s look at the frequency response (using fast Fourier transforms, FFTs) of the two converters as shown below. Note the difference in the noise floor between the two ADCs – big change! Recall that these are ideal ADCs with no error sources in time or amplitude. The difference is all from the difference in resolution.
Now let’s put up some numbers. Treating quantization noise as white noise, it is fairly easy to calculate the signal-to-noise ratio (SNR). It can be calculated in closed form for a sine wave, or we can root-sum-square all the noise in the FFT and compare it to the signal power. Either way, after playing with the math we find:
SNR = 6.02N+1.76 dB for an N-bit ADC (or DAC)
The 4-bit ADC has SNR of only ~26 dB while the 16-bit ADC’s SNR is over 98 dB. To put this in perspective, consider that a quiet room may be around 50 dB in sound pressure level (SPL); the threshold of pain is around 120 dB, and maximum peaks for something like a close gunshot or loud jet engine may be 140 dB or more. Using 120 dB as a maximum, that’s 70 dB of dynamic range in our room (before we start hurting). Getting 70 dB requires about 11 bits; using 16 bits provides additional headroom for those really big peaks and quiet rooms. Just like analog systems, you really don’t want to hear clipping!
The SNR is the ratio between the signal and the total noise. The difference between the signal and the highest other (noise or distortion) peak is the spurious-free dynamic range (SFDR). Calculating the SFDR is more complex and there is not a simple solution (one solution uses Bessel functions, but they make my head hurt). For an ideal N-bit ADC, the SFDR is about 9N dB, or about 36 dB for a 4-bit and 144 dB for a 16-bit ADC. The noise floor in the 16-bit plot is higher than 144 dB because only 64k points were used in the FFT; more points would reduce the noise floor but the figures get big and hard to upload.
Some other interesting things can be seen in the frequency plots. Although the actual input frequency is not exactly 1 kHz to avoid spectral leakage (1), there is still some “clumping” of energy visible in the 4-bit plot. The clumps are not all harmonically related to the signal, creating an unpleasant sound (2), and contribute to “digital noise” that nobody seems to enjoy. With 16 bits, the noise floor is much smoother in addition to be being much lower. Aside: early delta-sigma converters also exhibited non-harmonic tones related to the modulator loop and digital filters. These tones contributed to the poor sound from those early converters, both ADCs and DACs. Modern designs use more advanced architectures and techniques that virtually eliminate those tones.
So, more bits yield higher resolution and a much lower noise floor. Higher sampling rates allow higher frequencies to be captured and, because filters can affect frequency relationships in the signals, facilitate lower-order filters with higher cut-off frequencies that reduce their impact in the desired signal (audio) band.
Enough for now! Feel free to ask questions; more to come. - Don
Notes:
(1) FFTs operate upon a finite data set. Spectral leakage occurs when the signal samples do not fit precisely within the FFT’s window, creating artificial “skirts” around the signal frequency. Window functions are used to smoothly roll off the data at the start and end of the sample set and reduce these skirts. To eliminate leakage, the input signal period must start and end exactly at the window boundaries. There are several schemes to ensure this; I used the routine in the IEEE’s Standard 1241 for ADC testing.
(2) We are more sensitive to distortion frequencies that are unrelated to the signal. A pure sine wave (pure tone) is a single spike in an FFT. A triangle wave, sort of a “buzzy” sine wave, has only odd harmonics (multiples of the signal frequency). A square wave, a nastier raspy buzz, also has only odd harmonics, but at a higher level than a triangle wave. Frequency spikes not harmonically related tend to “stick out” more and sound worse than harmonic spurs to our hearing. That's one reason intermodulation distortion, the distortion that happens when two signals mix (multiply) imperfectly (i.e. the multiplier is not perfectly linear), is often more important than harmonic distortion.
As an interesting aside, bipolar transistors have an exponential error characteristic and when operated differentially (as most circuits operate) exhibit mostly odd harmonics. Tubes have a factorial distortion series and thus have intrinsically lower distortion than bipolar transistors. Because they are typically used in single-ended circuits, tubes exhibit primarily second-order distortion and sound better to our ears when distorting. An ideal FET’s distortion is a square-law characteristic ending at the second-order term, providing the lowest theoretical distortion. In practice, higher-order terms are present, but FET’s still provide among the lowest distortion when properly biased. They do have other issues so are not a panacea, natch.
“If a function of time f(t) contains no frequencies higher than W Hertz, it is completely determined by giving the value of the function at a series of points spaced 1/2W seconds apart.”
Claude Shannon was researching information theory and the most efficient ways to transmit and recover information. Harry Nyquist, a controls expert, refined the theorem and gave us the well-known Nyquist frequency limit: the maximum bandwidth that can be captured by sampling at frequency fs is fbw < fs/2.
A few comments on the sampling theorem:
- It applies to an infinite series of samples of infinite precision (i.e. “analog” samples, or using an infinite number of bits). This is not quite digital…
- The theorem relates to signal bandwidth, not its maximum frequency. For example, a cell phone band only 30 kHz wide but centered at 1 GHz (10^9 Hz) can in theory be recovered by a sampler operating at just over 60 kS/s (60,000 samples per second). The sampler must have 1 GHz input bandwidth, and all other signals must be filtered out. I will not discuss bandpass sampling further here.
- Frequencies above Nyquist are still captured by an ideal sampler, but their frequency content is folded, or aliased, so the signals fall within the fs/2 region. Thus frequency information is lost, but amplitude information is not. To prevent aliasing, there must be no frequency >= fs/2, which implies filters are needed before the analog to digital converter (ADC).
- The theorem works on the output (DAC) side as well, though the DAC can (and does) generate higher-frequency components than fs/2 without aliasing since they occur after sampling has taken place.
- The theorem itself does not describe practical implementation.
Most ADCs first convert a signal into discrete (quantized) time values using a track-and-hold (T/H) circuit, then quantize the amplitude to produce a digital signal. Thus we go from signals continuous in time and amplitude, to discrete time and continuous amplitude, and finally to digital signals having discrete time and amplitude. An ADC typically includes the T/H so we don’t see that intermediate step. However, sampling errors in time and amplitude are important in achieving a high-quality digital result.
The figure below shows a ramp input signal before (middle) and after (bottom) sampling by a T/H. The clock is high to track the signal, and low to hold. A perfect T/H instantly follows the signal when in track mode, and perfectly maintains the signal value in hold mode. There are a myriad of non-ideal effects in real systems including noise, nonlinearity (distortion), clock and signal feed through, finite bandwidth and acquisition time, hold-mode droop, glitches when changing state, etc. For now, just knowing what happens in a T/H is enough. Not all ADCs include a T/H, combining time sampling with amplitude quantization in one step. (Click on the figure to see bigger -- I shrunk them down to upload.)
After the T/H a quantizer converts the held values to discrete amplitude values. The resolution of the quantizer, and thus the complete ADC, is expressed in bits – numbers to the base two. One bit has two levels (2^1 = 2); four bits, 16 levels (2^4), etc. A 16-bit ADC has 65,536 discrete amplitude steps – quite a few, but a long way from infinite. The figure below shows a 1 kHz signal sampled at 44.1 kS/s (44.1 kHz, CD rate) by a 4-bit ADC. Very low resolution, but makes it easy to see what happens. The input is in red and output in blue. The output has levels from 0 to 15 (16 different values, or least-significant bits, lsbs). The error signal (dashed line) ties to the right-hand Y axis and for this perfect ADC ranges from -0.5 to +0.5 lsbs. Note the random appearance of the error signal; for an ideal ADC this is very close to (and generally treated as) simple white noise. This error is the quantization noise.
Stepping up to 16 bits give us the plot below. The number of steps is the same because the sampling time has not changed. However, the amplitude resolution is much finer (notice the output more closely follows the input). The error curve is a bit misleading since it is in lsbs; the error is actually only 1/4096 the size of the 4-bit ADC’s error! (The difference between 4 and 16 bits is 12 bits, and 2^12 = 4096.) I thought about plotting the two error curves together, but by eye the 16-bit error is essentially a flat line at the same scale as the 4-bit error signal.
To really see the difference in resolution, let’s look at the frequency response (using fast Fourier transforms, FFTs) of the two converters as shown below. Note the difference in the noise floor between the two ADCs – big change! Recall that these are ideal ADCs with no error sources in time or amplitude. The difference is all from the difference in resolution.
Now let’s put up some numbers. Treating quantization noise as white noise, it is fairly easy to calculate the signal-to-noise ratio (SNR). It can be calculated in closed form for a sine wave, or we can root-sum-square all the noise in the FFT and compare it to the signal power. Either way, after playing with the math we find:
SNR = 6.02N+1.76 dB for an N-bit ADC (or DAC)
The 4-bit ADC has SNR of only ~26 dB while the 16-bit ADC’s SNR is over 98 dB. To put this in perspective, consider that a quiet room may be around 50 dB in sound pressure level (SPL); the threshold of pain is around 120 dB, and maximum peaks for something like a close gunshot or loud jet engine may be 140 dB or more. Using 120 dB as a maximum, that’s 70 dB of dynamic range in our room (before we start hurting). Getting 70 dB requires about 11 bits; using 16 bits provides additional headroom for those really big peaks and quiet rooms. Just like analog systems, you really don’t want to hear clipping!
The SNR is the ratio between the signal and the total noise. The difference between the signal and the highest other (noise or distortion) peak is the spurious-free dynamic range (SFDR). Calculating the SFDR is more complex and there is not a simple solution (one solution uses Bessel functions, but they make my head hurt). For an ideal N-bit ADC, the SFDR is about 9N dB, or about 36 dB for a 4-bit and 144 dB for a 16-bit ADC. The noise floor in the 16-bit plot is higher than 144 dB because only 64k points were used in the FFT; more points would reduce the noise floor but the figures get big and hard to upload.
Some other interesting things can be seen in the frequency plots. Although the actual input frequency is not exactly 1 kHz to avoid spectral leakage (1), there is still some “clumping” of energy visible in the 4-bit plot. The clumps are not all harmonically related to the signal, creating an unpleasant sound (2), and contribute to “digital noise” that nobody seems to enjoy. With 16 bits, the noise floor is much smoother in addition to be being much lower. Aside: early delta-sigma converters also exhibited non-harmonic tones related to the modulator loop and digital filters. These tones contributed to the poor sound from those early converters, both ADCs and DACs. Modern designs use more advanced architectures and techniques that virtually eliminate those tones.
So, more bits yield higher resolution and a much lower noise floor. Higher sampling rates allow higher frequencies to be captured and, because filters can affect frequency relationships in the signals, facilitate lower-order filters with higher cut-off frequencies that reduce their impact in the desired signal (audio) band.
Enough for now! Feel free to ask questions; more to come. - Don
Notes:
(1) FFTs operate upon a finite data set. Spectral leakage occurs when the signal samples do not fit precisely within the FFT’s window, creating artificial “skirts” around the signal frequency. Window functions are used to smoothly roll off the data at the start and end of the sample set and reduce these skirts. To eliminate leakage, the input signal period must start and end exactly at the window boundaries. There are several schemes to ensure this; I used the routine in the IEEE’s Standard 1241 for ADC testing.
(2) We are more sensitive to distortion frequencies that are unrelated to the signal. A pure sine wave (pure tone) is a single spike in an FFT. A triangle wave, sort of a “buzzy” sine wave, has only odd harmonics (multiples of the signal frequency). A square wave, a nastier raspy buzz, also has only odd harmonics, but at a higher level than a triangle wave. Frequency spikes not harmonically related tend to “stick out” more and sound worse than harmonic spurs to our hearing. That's one reason intermodulation distortion, the distortion that happens when two signals mix (multiply) imperfectly (i.e. the multiplier is not perfectly linear), is often more important than harmonic distortion.
As an interesting aside, bipolar transistors have an exponential error characteristic and when operated differentially (as most circuits operate) exhibit mostly odd harmonics. Tubes have a factorial distortion series and thus have intrinsically lower distortion than bipolar transistors. Because they are typically used in single-ended circuits, tubes exhibit primarily second-order distortion and sound better to our ears when distorting. An ideal FET’s distortion is a square-law characteristic ending at the second-order term, providing the lowest theoretical distortion. In practice, higher-order terms are present, but FET’s still provide among the lowest distortion when properly biased. They do have other issues so are not a panacea, natch.
Last edited: