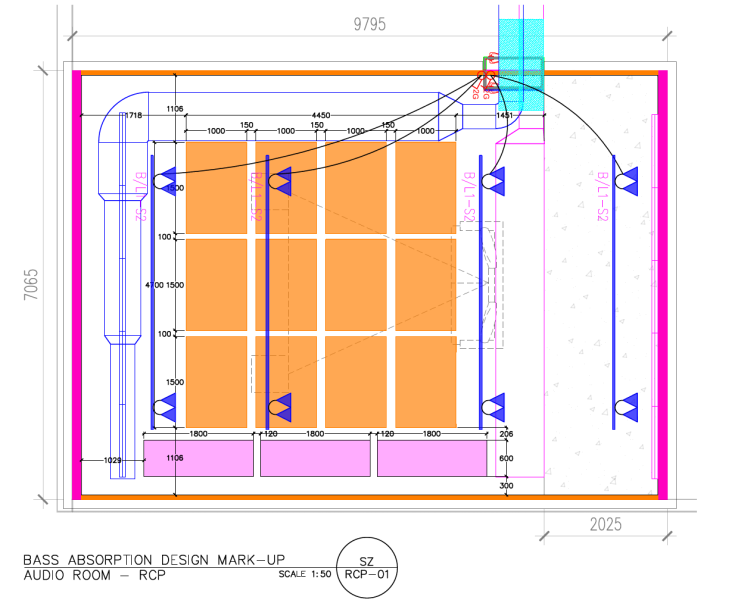
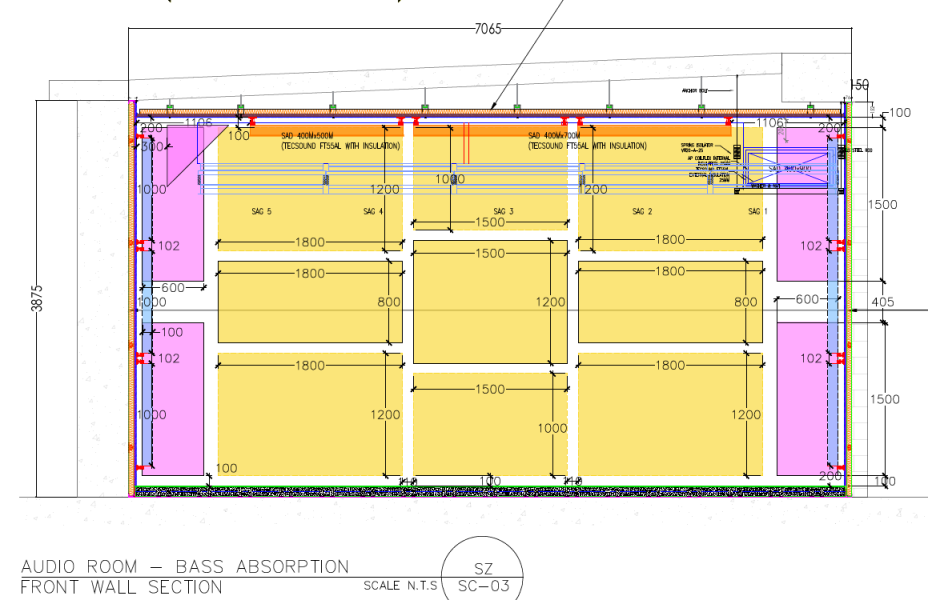
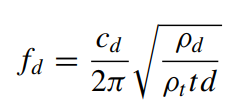Since we are going down the VPR rabbit hole, I thought i would discuss the formulas for the plate bending modes.
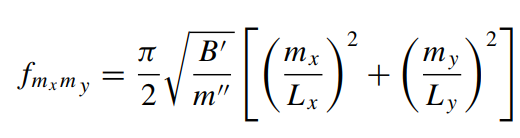
Where:
m'' is the mass per unit area of the plate
B' is defined below
pi/2 = 1.570795
Lx is the length of the plate
Ly is the width of the plate
Mx and My are the modes. these are integer values (1,2,3,4 ....) For the first mode you would input Mx =1 and My = 1.
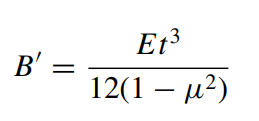
Where:
E is the modulus of elasticity of the material of the plate
t is the thickness of the plate
u is Poisson's ratio for the material of the plate.
E of steel is 30E6 PSI
E of Aluminum is 10E6 PSI
u of steel is about 0.3
u of Aluminum is about 0.33
Notice there is nothing about the foam in this equation. The purpose of the foam is to damp the vibration of the plate. The foam needs to be strong enough to support the plate. The plate needs to be in strong contact with the foam (i.e. glued with elastomeric glue). properties of the foam only come into play if you are wanting to use the "mass-spring" system to target a specific frequency. This is always problematic, and I suggest ignoring it.
To me it was insightful to rearrange the formula a little. Do some algebra of B'/m'' and you will see that the formula reduces to:
SQRT (B'/m'') = t * SQRT [ (E/D)*(1/(1-u^2) ] Where D is the density of the plate material.
Density of Steel = 0.284 lb/in^3
Density of Aluminum = 0.0976 lb/in^3
E/D for Steel = 105.6E6 in
E/D for Aluminum = 102.5E6 in
Sqrt (B'/m'') for steel = 10,772 * t
Sqrt (B'/m'') for Aluminum = 10,725 * t
(Of course, you may want to check my math)
The point is that Aluminum and Steel have basically the same modal frequencies. This is relevant as Aluminum is much lighter than steel, thus making it easier for the foam to support the weight. It also makes it easier to handle during the construction process. The lighter material should also be easier to acoustically excite.
A couple other points to make are that as the thickness of the plate increases the lowest frequency will go up. Keep the plate thin. As the dimension of the plate goes up the frequency goes down. Make the panel large(ish). To spread out the frequencies make the length and width different. Assuming you are going to put more than one of these in your room then you could make different sizes that target different frequencies. Also the thickness of the foam doesn't matter when only using the plates modal frequencies. 1" or 2" foam is sufficient. The closer you get the plate to the wall the better because the pressure is highest right at the wall's surface. If you want a broadband absorber you can glue foam to the front of the plate as well.
Again, these are stupid simple to make. Simply, buy the foam and the plate. Glue the plate to the foam. Hang it on the wall where there is high pressure.
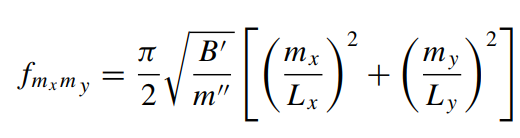
Where:
m'' is the mass per unit area of the plate
B' is defined below
pi/2 = 1.570795
Lx is the length of the plate
Ly is the width of the plate
Mx and My are the modes. these are integer values (1,2,3,4 ....) For the first mode you would input Mx =1 and My = 1.
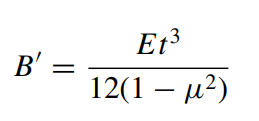
Where:
E is the modulus of elasticity of the material of the plate
t is the thickness of the plate
u is Poisson's ratio for the material of the plate.
E of steel is 30E6 PSI
E of Aluminum is 10E6 PSI
u of steel is about 0.3
u of Aluminum is about 0.33
Notice there is nothing about the foam in this equation. The purpose of the foam is to damp the vibration of the plate. The foam needs to be strong enough to support the plate. The plate needs to be in strong contact with the foam (i.e. glued with elastomeric glue). properties of the foam only come into play if you are wanting to use the "mass-spring" system to target a specific frequency. This is always problematic, and I suggest ignoring it.
To me it was insightful to rearrange the formula a little. Do some algebra of B'/m'' and you will see that the formula reduces to:
SQRT (B'/m'') = t * SQRT [ (E/D)*(1/(1-u^2) ] Where D is the density of the plate material.
Density of Steel = 0.284 lb/in^3
Density of Aluminum = 0.0976 lb/in^3
E/D for Steel = 105.6E6 in
E/D for Aluminum = 102.5E6 in
Sqrt (B'/m'') for steel = 10,772 * t
Sqrt (B'/m'') for Aluminum = 10,725 * t
(Of course, you may want to check my math)
The point is that Aluminum and Steel have basically the same modal frequencies. This is relevant as Aluminum is much lighter than steel, thus making it easier for the foam to support the weight. It also makes it easier to handle during the construction process. The lighter material should also be easier to acoustically excite.
A couple other points to make are that as the thickness of the plate increases the lowest frequency will go up. Keep the plate thin. As the dimension of the plate goes up the frequency goes down. Make the panel large(ish). To spread out the frequencies make the length and width different. Assuming you are going to put more than one of these in your room then you could make different sizes that target different frequencies. Also the thickness of the foam doesn't matter when only using the plates modal frequencies. 1" or 2" foam is sufficient. The closer you get the plate to the wall the better because the pressure is highest right at the wall's surface. If you want a broadband absorber you can glue foam to the front of the plate as well.
Again, these are stupid simple to make. Simply, buy the foam and the plate. Glue the plate to the foam. Hang it on the wall where there is high pressure.
Last edited: