Amplifier clipping has been cited as the cause of audible distortion, destruction of speakers (especially tweeters), and total annihilation of the known universe. More or less. In fact, clipping does cause distortion that adds significant high-frequency content not in the original signal, and does present higher power to the speaker.
To address power, a pure sine wave (undistorted signal) with peak amplitude A has an RMS value of A/sqrt(2) or 0.7071*A. A heavily clipped sine wave approximates a square wave, and thus has RMS value of A, about 30% higher. Assuming voltage is clipped, the square wave has twice the power of the pure sine wave since power is related to voltage squared. That is, a heavily clipped signal puts up to twice the power into the speaker as an unclipped signal of the same (peak) amplitude. Less-clipped signals will not have as large a power increase, naturally.
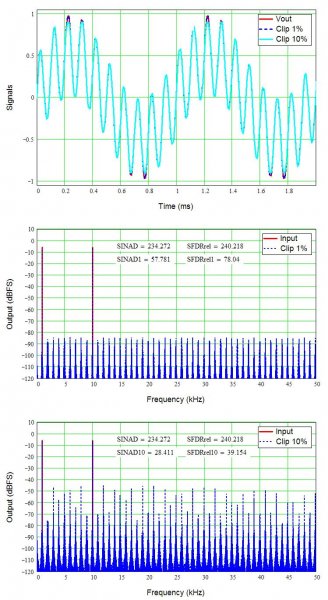
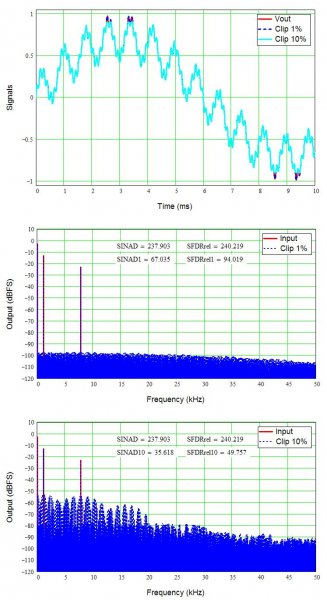
We already know square waves can be made from a series of sine waves (see related thread), thus clipping must add higher frequency content to create those sharply flattened peaks. The figure below shows a pure 1 kHz sine wave, and clipped by 1% and 10%. The spectral diagrams (FFTs) show the resulting frequency content up to 50 kHz, and include the calculated SINAD (signal to noise and distortion) and SFDR (spurious-free dynamic range, the distance from the signal to the highest distortion spur in dB).
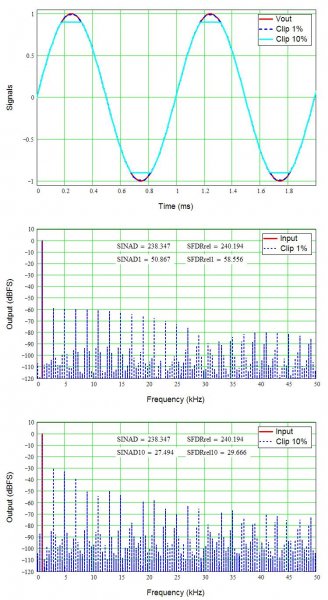
The unclipped signal is a single spike at 1 kHz in the FFT. SINAD and SFDR around 240 dB represent the limits of the math program (resolution of the input signal). With 1% clipping, we see numerous spurs extending to 50 kHz (and well beyond, but I chopped the plot there), and now SINAD is only 51 dB and SFDR around 58 dB. While significant, this is probably inaudible, especially in the presence of more complicated musical (or movie) signals. However, you can probably hear the clipping as a low but harsh buzzing sound if you were to play this as a test tone.
Notice 10% clipping reduces SINAD to 27.5 dB and SFDR to 29.7 dB, still fairly small relative to the signal but high enough that I suspect most of us can hear it even with the music playing. More complicated signals will produce more complex distortion but the idea is the same; added high-frequency content and higher power than in the original signals.
HTH - Don
To address power, a pure sine wave (undistorted signal) with peak amplitude A has an RMS value of A/sqrt(2) or 0.7071*A. A heavily clipped sine wave approximates a square wave, and thus has RMS value of A, about 30% higher. Assuming voltage is clipped, the square wave has twice the power of the pure sine wave since power is related to voltage squared. That is, a heavily clipped signal puts up to twice the power into the speaker as an unclipped signal of the same (peak) amplitude. Less-clipped signals will not have as large a power increase, naturally.
We already know square waves can be made from a series of sine waves (see related thread), thus clipping must add higher frequency content to create those sharply flattened peaks. The figure below shows a pure 1 kHz sine wave, and clipped by 1% and 10%. The spectral diagrams (FFTs) show the resulting frequency content up to 50 kHz, and include the calculated SINAD (signal to noise and distortion) and SFDR (spurious-free dynamic range, the distance from the signal to the highest distortion spur in dB).

The unclipped signal is a single spike at 1 kHz in the FFT. SINAD and SFDR around 240 dB represent the limits of the math program (resolution of the input signal). With 1% clipping, we see numerous spurs extending to 50 kHz (and well beyond, but I chopped the plot there), and now SINAD is only 51 dB and SFDR around 58 dB. While significant, this is probably inaudible, especially in the presence of more complicated musical (or movie) signals. However, you can probably hear the clipping as a low but harsh buzzing sound if you were to play this as a test tone.
Notice 10% clipping reduces SINAD to 27.5 dB and SFDR to 29.7 dB, still fairly small relative to the signal but high enough that I suspect most of us can hear it even with the music playing. More complicated signals will produce more complex distortion but the idea is the same; added high-frequency content and higher power than in the original signals.
HTH - Don