Relating Distortion Percent (%) to dB

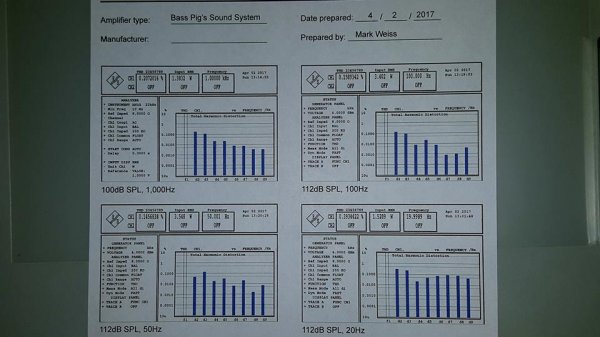
This post provides a quick comparison of how a distortion percentage relates to dynamic range in dB. That is, if an amplifier has 1% distortion, what does that mean? How soft (or loud) is 1%?

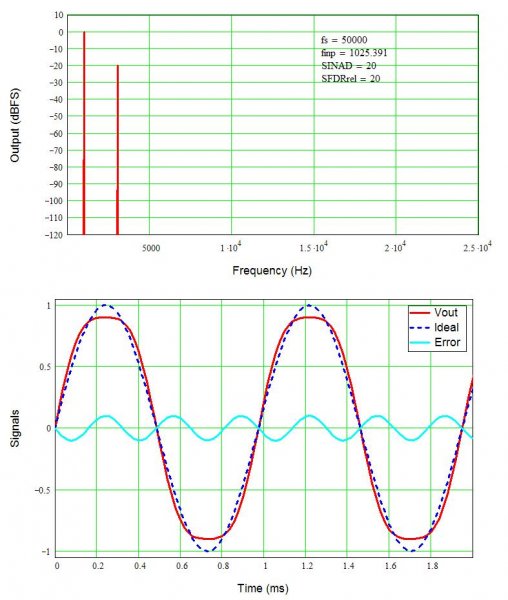
Figure 1 shows a 1 kHz voltage signal with 1% second harmonic distortion (HD2) added. The spectral analysis (FFT, fast Fourier transform) shows the second harmonic at 40 dB below (-40 dB) the (0 dB) signal. So, 1% distortion is 40 dB below the signal level. Recall that dB = 20log(x), 1% is 1/100 = 0.01, and 20log(0.01) = -40 dB. Aside: Power goes as 10log(x), so 1% distortion in power (Watts) is only -20 dB. In SPL (dB/W), 20 dB is about the difference between say a pretty loud sound (80 dB) and a normal conversational volume (60 dB). Since we are in voltage (maybe a preamplifier output before the power amp), 40 dB takes you from that loud sound down to a fairly quiet room, say a library.



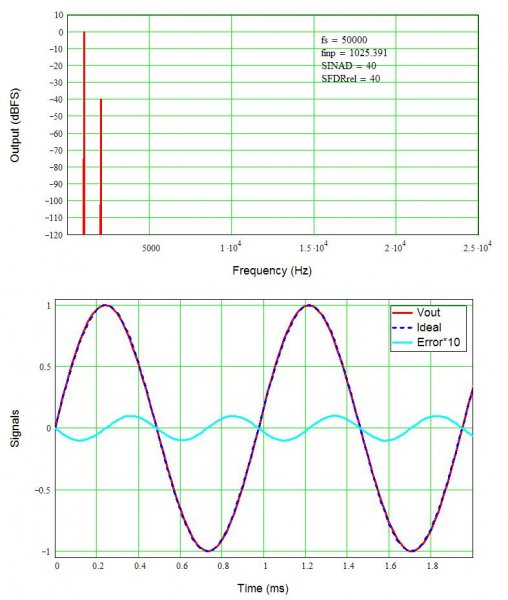
The lower plot shows an ideal sine wave, the signal with 1% distortion, and the difference (error) signal multiplied by 10 to make it easier to see. By eye, I cannot see any difference in the ideal input signal and output with 1% distortion (Vout). Because the error is purely second harmonic distortion, notice there are twice as many cycles in the error as in the input signal.

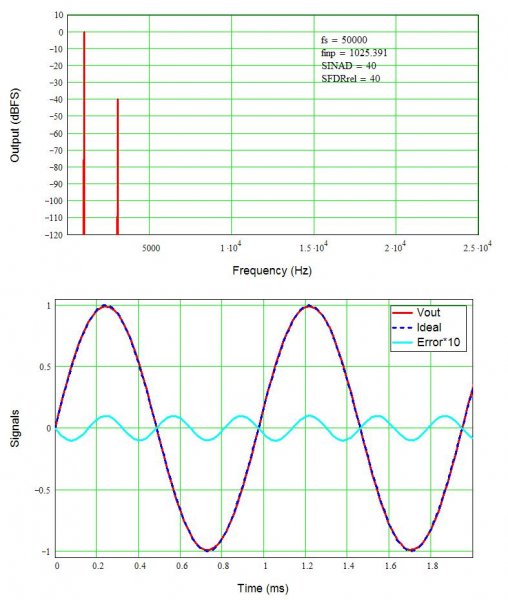
The figure below shows the same 1% distortion but now it is third harmonic distortion (HD3). The HD3 spur is -40 dB, but notice there are now three error cycles for each full cycle (0-up-0-down-o) of the signal. And again, I can’t see anything by eye (maybe you can).



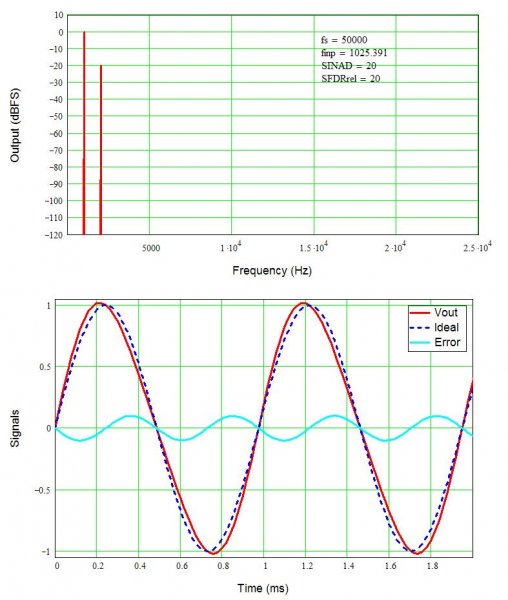
Just for grins, and for something to see, the following two pictures show 10% HD2 and HD3. As expected the harmonic terms are now only 20 dB below the signal. What is interesting is how the high level of distortion changes the look of the waveforms. Second harmonic distortion does not change the picture too much, but third harmonic distortion causes the peaks to flatten, sort of like a soft square wave. Even harmonics tend to sound more pleasant than odd harmonics, adding a bit of edge to the sound while odd harmonics create a raspy buzz.




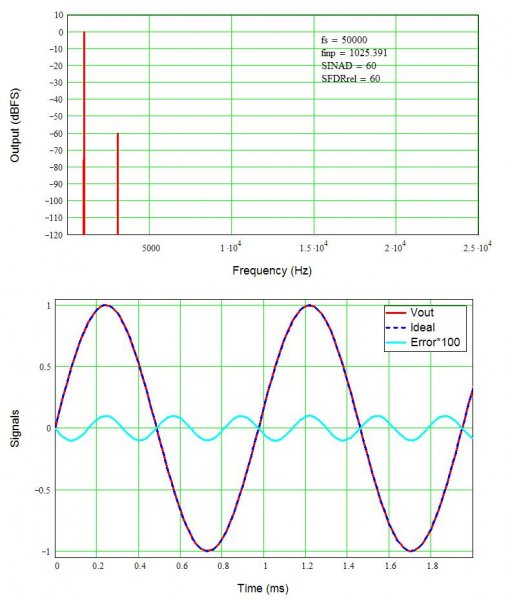
Last is a figure showing 0.1% HD3, with a spur 60 dB below the signal. A factor of ten in distortion changes the level by 20 dB (in voltage; a 10x change in power is 10 dB).



Finally, here’s a table showing the relationship among distortion in percent and dB in voltage (or current) and power. The dominant source of distortion in most systems is the speakers, which often run 1% or more in the midrange even for good ones, and 10% or more for large low-frequency signals. Amplifiers usually run in the 0.1 – 1% range, and preamps often 0.01% or better.

Distortion (%) Relative Voltage Level (dB) Relative Power Level (dB)
0.01 -80 -40
0.05 -66 -33
0.10 -60 -30
0.50 -46 -23
1.00 -40 -20
5.00 -26 -13
10.0 -20 -10

<Could not figure out how to clean up the table alignment, sorry!>

Hopefully this will help relate those distortion percentages to the dB specifications used for SNR, SPL, and so forth.

You bet! In Days Gone By, 1% was used to distinguish HiFi from run-of-the-mill systems. I do not recall the history off-hand so do not know if it was determined by what listeners could hear in tests or if it was a relatively arbitrary number. I do know from my past life in audio, given musical material through a speaker system, most of us cannot tell if there's 1% distortion. On test tones, perhaps, particularly on a two-tone test where IMD comes into play. For example 3rd-order IMD is about three times the amplitude of 3rd-order harmonic distortion (HD) and is thus about twice as loud, and because it adds non-harmonic tones we hear IMD more readily. IMD2 is about twice the amplitude of HD2. IIRC, HD on sine waves could be detected around 1%, IMD as low as 0.1%, depending upon frequency (we are less sensitive down low). I was thinking of doing a similar post for IMD but ran out of time, maybe later.

Note the ear/mind is good at integrating sounds out of the noise floor, meaning in tests we can actually pull out tones below the noise floor. (For the record, radar and communication systems are also good at pulling signals out of the noise.) Modern audio systems have such a low noise floor that it doesn't really matter, but in fact you can hear tones even if they are below the hiss from your amps. However, a 1% spur is harder to hear when it is under a 100% signal, a point sometimes lost in these discussions. And perhaps much harder when surrounded by a forest of other tones in a musical selection.

Disclaimer: It has been a long time since I did any research on how much distortion we can hear, masking effects, and such so this post (unlike the first which is pure number-crunching) is all very much based upon my foggy memory and opinions. How we perceive distortion is fascinating and something well worth spending more effort to learn, but that is not where this thread started. I simply wanted to give folk a picture since I tend to visualize everything.

A bit off-topic re. this thread, but IIRC user focus groups soundly panned the idea of a 5-point as too hard to hook up and get out of and too "intrusive". Never mind it's what racers use, and they like getting in and out quickly... It is also more hardware and cost, but compared to an airbag? Come on!

I think that speakers exhibit many orders of magnitude greater than that. And that dynamic range is more important than distortion in a lot of cases.

BTW, spurious-free dynamic range (signal to highest spurious signal) goes as 9N, not 6N, in an ideal converter. So , the peak spur would be 9*16 = 144 dB down for a 16-bit converter, or about 0.0000063%. Most converters do not approach that 9N limit, and struggle to attain close to ideal SNR even at the 16 - 18-bit level. Those two little words "perfectly converted" are killer...

I remember the days when to be "best" you had to have 0.001% THD or better. Eventually we discovered that large amounts of negative feedback can cover and cause other issues... Not to say no feedback doesn't have its own set of problems. A little is good, a lot can kill, and so can none.

<Hand-waving alert>

See my other threads for a more thorough description of SNR and SFDR. For now, for an ideal N-bit converter, the signal-to-noise ratio (SNR) set by quantization noise is about 6N dB (6.021N+1.76 dB) for a full-scale signal. This is the number you get by integrating (adding, sort-of) all the noise spurs (the "grass" of the noise floor) in the converter's bandwidth and compare it to the signal level. It hopefully makes sense that, sense SNR uses the sum total of all noise, that any individual noise spur must be much lower than the total. In fact, the distance from the signal (at full-scale) to the highest noise spur is about 9N dB (the spurious-free dynamic range, SFDR). Sum all those little spurs ~9N dB (or more) down, and the result is about 6N dB. easier to show with pictures.

The quantization noise floor is a fixed thing, relatively constant no matter the signal. A data converter is not a linear system. In contrast, the distortion of an analog amplifier goes down as the signal is reduced. So, at rated power the amplifier might put out 1% distortion, or 0.1%, whatever. However, as the signal level goes down, so does the distortion, and in fact it falls faster than the signal so the SFDR increases as the signal level decreases. An analog amplifier gets more linear as the signal is reduced. Eventually the noise floor is reached so THD+N flattens out, then rises as the signal gets closer to and below the noise floor. At 0.1 W your amp may indeed have below 0.001% distortion.

And, we can hear through a lot more distortion than most people realize. Remember the dynamic range of most good amplifiers is 100 dB or so, so they do meet our 16-bit requirement.

HTH - Don